FECHA: Semana de 5 al 9 de abril
Tema: Fracciones
Fracciones
Una fracción es un número que representa una o varias partes
de una unidad o de un conjunto.
Una fracción tiene dos términos: El numerador y el
Denominador.
Denominador: Indica el número
de partes iguales en que se divide la unidad o el conjunto.
Numerador: Indica el número
de partes iguales que se toman de la unidad o conjunto.
Pintar las partes que me indica el numerador y luego colocar
a cada fracción sus términos.
Actividad virtual
Colocar los términos a las siguientes fracciones.
Actividad en casa: Completar en los cuadros
correspondientes lo que indica cada fracción.
(Cuaderno de ejercicios. )
FECHA: Semana de 12 al 16 de
abril
Tema: Fracciones
Lectura de fracciones
Las fracciones se lee de acuerdo con el
denominador.
Colocar al frente como se
lee cada fracción.
Clases de fracciones
Las fracciones se clasifican en:
Fracciones propias: Son aquellas menores que la unidad. Tienen el numerador menor que el
denominador.
Fracciones unidad: Son aquellas iguales a la unidad. Tienen el numerador igual al
denominador.
Fracciones impropias: Son aquellas mayores que la unidad. Tienen el numerador mayor que el denominador.
Números mixtos
Toda fracción impropia se presenta como un
numero mixto. Un numero0 mixto esta formado por una parte entera y una fracción
propia.
Actividad para loa casa
Pasar las siguientes fraccio9nes propias a números mixtos.
FECHA: Semana del 19 al 23 de abril
Tema: conversión de fracciones impropias a
números mixtos
conversión de fracciones impropias a números mixtos
para convertir una fracción impropia a un
número mixto se utiliza la división.
Como te habrás dado cuenta, para transformar
una fracción impropia en un número mixto, se debe dividir el numerador entre el
denominador. El cociente será la parte
entera del número, y el residuo será el numerador de la fracción restante, que
tendrá el mismo denominador que la original.
Tomemos como ejemplo la fracción. 22 quintos
Al realizar la operación, 22 quintos obtenemos
como resultado 4 y sobran 2 . Es decir,
el cociente es cuatro y el residuo es dos.
Representación grafica en la recta numérica
las fracciones también se pueden representar
en la recta numérica.
Actividad
virtual
Representar las siguientes fracciones en la
recta numérica.
Cinco medios Siete cuartos Ocho quintos Diez cuartos
Ocho tercios seis cuartos dieciséis
cuartos Doce sextos
Catorce quintos Quince novenos
Simplificación de fracciones
Simplificar una fracción es reducir tanto su
numerador como su denominador a otra fracción con números menores. Esa fracción
que obtenemos es una fracción equivalente a la inicial, esto quiere decir que
representa la misma cantidad pero tiene distinta representación.
Por ejemplo: vamos a ver el caso de la
fracción cuatro octavos.
Nos hemos ayudado de una barra para ver la fracción. Está dividida en 8
partes y se han coloreado 4. A simple vista podemos darnos cuenta de que
representa la mitad de la barra, esto es, que cuatro octavos equivalen a un
medio, pero no solo eso, cuatro octavos es equivalente a una infinidad de
fracciones.
En este caso, te voy a pedir que te fijes en
que las dos fracciones de la derecha, tienen algo en común, representan la
misma cantidad que cuatro octavos, pero con un menor número de partes:
Actividad virtual
Simplificar las siguientes fracciones.
Actividad en casa:
Fecha:
Semana del 26 al 30 de abril
Tema: adición y sustracción de fracciones con
igual denominador
Suma de fraccionarios con igual denominador
Para sumar fracciones
con el mismo denominador se tienen que sumar los numeradores dejando el mismo
denominador.
Como las 2 fracciones
tienen el mismo denominador, lo que tenemos que hacer es dejar el mismo
denominador, que es 4, y sumar los numeradores:
3 + 2 = 5
Y el resultado de la
suma de fracciones es:
Suma de fraccionarios con diferente denominador
Para calcular la suma de
este tipo de fracciones tendremos que multiplicar los denominadores para hallar
el denominador de la fracción resultante, y para conseguir el numerador
tendríamos que multiplicar el numerador de una de las fracciones por el
denominador de la otra y viceversa, y posteriormente, sumar el resultado.
Vamos a poner un ejemplo.
Sumemos 11/10 + 2/3.
Los denominadores son 10
y 3, que son diferentes y no tienen divisores en común, por lo que tendremos
que multiplicarlos entre ellos. 10 x 3 = 30, por lo que 30 será el denominador
de la fracción resultante.
Para calcular el
numerador, tendremos que multiplicar 11 x 3 = 33 y 10 x 2 = 20, y sumar los
resultados, 33 + 20 = 53, que sería el numerador de la fracción obtenida.
El resultado final de la
suma sería: 53/30
Resolver los siguientes fraccionarios.
Resta de fraccionarios de diferente denominador
Para calcular la resta de este tipo de
fracciones tendremos que multiplicar los denominadores para hallar el
denominador de la fracción resultante, y para conseguir el numerador tendríamos
que multiplicar el numerador de una de las fracciones por el denominador de la
otra y viceversa, y posteriormente, restar el resultado.
Actividad virtual
Actividad en casa
Resolver en el cuaderno de ejercicios-
Fecha:
Semana del 3 al 7 de mayo
Tema:
Multiplicación y división de números fraccionarios
La
Multiplicación de fracciones se realiza escribiendo como numerador el producto
de los numeradores, y como denominador, el producto de los denominadores. Esto
lo podemos ver en el siguiente esquema:
En la
multiplicación de fracciones, la segunda fracción equivale a la parte que se
toma de la primera fracción. Para comprender esto mejor, podemos tomar en
consideración una fracción que equivalga a un número entero por ejemplo, 4/2,
que es igual a 2. Si lo multiplicamos por 1/4, esto
equivale a tomar la cuarta parte de 4/2:
4/2 X 1/4 = 4X1/2X4 = 4/8
Reduciendo
a fracciones comunes:
4/8 = 2/4 = ½
Ejemplos:
Actividad
virtual.
Método 1 de
división de fracciones: Multiplicar en cruz
Este método consiste en multiplicar el numerador de la primera fracción
por el denominador de la segunda y el resultado escribirlo en el numerador de
la fracción resultante.
Por otro lado, multiplicamos el denominador de la primera fracción por
el numerador de la segunda y el resultado lo escribimos en el denominador de la
fracción resultante.
Por último se simplifica la fracción final.
Por ejemplo, para dividir las fracciones 3/4 entre 6/10.
Multiplicamos el numerador de la primera (3) por el denominador de la
segunda (10). De esta manera, nos queda en el numerador de la fracción final
3×10 = 30
Por otro lado, multiplicamos el denominador de la primera (4) por el
numerador de la segunda (6). De esta manera, nos queda en el denominador de la
fracción final 4×6 = 24
El último paso es simplificar la fracción. Como los dos números son
múltiplos de 6 podemos dividir el numerador y el denominador entre 6.
30 : 6 = 5
24 : 6 = 4
Por lo tanto, el resultado de la división es 5/4
Método 2 de división de fracciones: Invertir y multiplicar
1. Invertir la segunda fracción, es decir, cambiar el numerador por el
denominador y viceversa.
2. Simplificar cualquier numerador con cualquier denominador.
3. Multiplicar en línea.
Por ejemplo, vamos a dividir 12/5 entre 6/4.
Paso 1: Invertimos la segunda fracción 6/4. Esto se
convierte en 4/6
Paso 2: multiplicamos numerador con numerador y
denominador con denominador
Actividad virtual
Resolver
Evaluación de fraccionarios
2.
Resolver
Colocar
loas siguientes fracciones en la recta numérica
Buena
suerte. Lea y revise bien antes de contestar.
Fecha:
Semana del 10 al 14 de mayo
Tema:
Números decimales
Fracciones decimales
Una fracción decimal es aquella en la cual el número de abajo, o sea el denominador, es una potencia de diez, como sería 10; 100; 1000; 10000, etc. Es posible entonces escribir fracciones que sean decimales con un punto decimal y sin el denominador. Esto facilita enormemente el calcular las operaciones, tales como las sumas o multiplicaciones de las fracciones. Los números decimales son en si un tipo de número fraccionario. Por ejemplo, el decimal 0.5 representa exactamente la fracción 5/10. La fracción 43/100 es también la representación de un decimal, es lo mismo entonces que 0.43. Veamos algunos otros ejemplos más claros:
Actividad virtual
Convertir
las siguientes fracciones a números decimales.
Números decimales
Leer l siguiente cuento y luego pegarlo en el cuaderno de
ejercicios-
Érase
una vez dos hermanos que vivían en un bosque muy lejano. El más pequeño se
llamaba Entero "el despistado " y la pequeña se
llamaba Decimal "la alocada". Un día Entero dijo
a su hermana:
-Decimal,
deberás de dejar de jugar en el parque con tu amiga, Coma. Siempre
está intentando separarnos y hacer de nosotros personas nuevas. Además, esta
noche seguramente venga el lobo y debemos estar protegidos.
Cuando
llegó la noche, Entero tenía hecha una casa de paja y Decimal,
una casa de madera. El lobo se acercaba a sus casas de manera silenciosa, y
como siempre solía hacer, le encantaba molestarlos. Sabía que dormirían desde
primera hora de la tarde, por lo que cuando quiso llegar a sus casas, nada
ocurrió como el lobo esperaba.
-
Lo intentaré, lo intentaré y tu sueño de un grito pararé.
La
pequeña Decimal al oír las palabras del lobo, se despertó del
que hasta ese momento estaba siendo el mejor sueño de la semana. Fue corriendo
a casa de su hermano Entero, donde se sintió a salvo, pero….. el
lobo gritando con fuerza volvió a repetir:
-
Lo intentaré, lo intentaré y tu sueño de un grito pararé.
Los
dos hermanos asustados tomaron la decisión más inesperada. Tuvieron que ir a
casa de Coma, para ahí poder continuar con los dulces y largos
sueños. Coma se sorprendió al verlos en la puerta de su casa,
teniendo en cuenta lo sucedido por la mañana en el parque. Sorprendentemente
para los dos hermanos, Coma no puso ningún problema y les
abrió las puertas de su casa.
Cuando
ya habían conseguido conciliar otra vez el sueño, escucharon aquella frase de
la que llevaban huyendo toda la noche.
-Lo
intentaré, lo intentaré y tu sueño de un grito pararé.
El
lobo lo intentó una y otra vez pero no pudo conseguirlo. En este momento se dio
cuenta que ya no tenía nada que hacer, dado que los tres juntos iban a ser más
fuertes que él.
En
ese momento, Decimal le dijo a su hermano la siguiente
frase:
- Espero
que hallas aprendido que no puedes hablar de las personas sin conocerlas antes.
Piensas que Coma quiere separarnos y así cambiar nuestro
valor, pero eso no es verdad. Coma también tiene derecho a
estar entre nosotros, puede que nos cambie el valor y que a partir de ese
momento nos cambien el nombre. ¿ Qué hay de malo? Ser diferentes también es
bueno y has en algunos momentos, ventajoso. Míralo desde ese punto de
vista Entero
Él
asintió, y a Coma se le puso una sonrisa más grande que el
arco que a veces cubría a Decimal del sol.
Colorín
colorado este micro-cuento se ha acabado.
Lectura de números decimales
Para leer un numero decimal se lee primero la parte entera, luego, la coma y por último, la parte decimal con el nombre de la posición que ocupa la última cifra. Ejemplo:
actividad virtual
Orden en los decimales
Actividad en casa
Ordenar las siguientes fracciones de mayor a
menor.
Pasar las siguientes fracciones a números
decimales
Semana del 18 al 21 de mayo
Tema: adición de números decimales
Para sumar números decimales, se escriben los sumandos uno debajo del otro, teniendo en cuenta que las comas decimales y las unidades del mismo orden queden alineadas. Luego, se realiza la operación.
Actividad virtual
345,56 + 45,8 + 345,67 + 45,2
3,456 +45, 56 + 456, 2
3,56 + 5567, 8+ 23,567 + 8
5,67 + 3,567+ 778,56
5,45
+ 4,56 + 678,45 + 8,90
sustracción de números decimales
Para restar números decimales se escribe el minuendo debajo del
sustraendo, de modo que correspondan las unidades del mismo orden. Si la
cantidad de cifras decimales n es igual, se completa con seros y se realiza la
operación.
Actividad en casa
Resolver los siguientes ejercicios
45,78 + 567,4 + 4.6
45,789 + 34.56 + 3.5 + 9
345, 67 + 45,6 + 12, 45 + 67
5,67+ 89,34 + 234, 5+ 90
45, 786- 45,67
678,45 – 56, 89
894, 56 – 56, 45
567, 23 – 356, 8
456, 5 – 234, 4
Áreas matemáticas
Semana del 6 al 10 de julio
Tema: Multiplicación e números decimales
Multiplicación de números
decimales
Para multiplicar números decimales, se realiza la operación como si
fueran números naturales. Luego en el resultado se cuentan de derecha a
izquierda, tantos lugares como cifras decimales tengan los factores. En este
lugar se escribe la coma. Ejemplo:

























































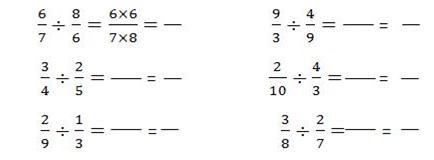

















No hay comentarios:
Publicar un comentario